No artigo sobre matrizes, estudamos a definição de matriz, sua representação e os tipos de matrizes que podemos encontrar, em nível de educação básica, ao longo da nossa jornada estudantil. É importante lembrar que representações organizadas de números em formas de tabelas já eram utilizadas em tempos muito remotos, a exemplo da Era Cristã. Porém, somente no Século XIX, com matemáticos como Cauchy, Cayley e Hamilton, é que nasceu a representação moderna das matrizes, e que se manteve até os dias atuais.
Neste trabalho, estudaremos a Matriz Transposta, mas sempre que precisar de maior clareza em relação à conceituação básica de matriz e da compreensão dos seus tipos, recomenda-se recorrer ao primeiro trabalho intitulado “Matrizes”, publicado neste portal.
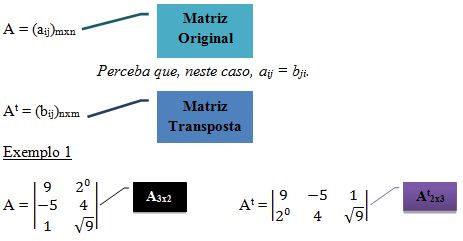
Matriz transposta
Tomando por base uma matriz A de ordem m x n, teremos a sua matriz transposta, indicada por At, invertendo as posições de m e n, isto é, n x m.
Em termos gerais, temos:
A 1ª linha de A tornou-se a 1ª coluna de At; a 2ª linha de A tornou-se a 2ª coluna de At; a 3ª linha de A tornou-se a 3ª coluna de At.
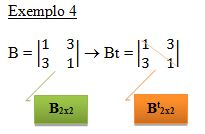
A 1ª linha de B tornou-se a 1ª coluna de Bt; a 2ª linha de B tornou-se a 2ª coluna de Bt.
Observação: Sempre que a matriz transposta At for igual à sua matriz quadrada A, dizemos que esta matriz A é uma Matriz Simétrica. Em resumo, se A = At, A é uma Matriz Simétrica.
Na Matriz Simétrica, os elementos são simétricos em relação a diagonal principal. Se A = (aij) é simétrica, temos aij = aji.
Neste caso, A = At, portanto A é uma matriz simétrica.
Obs.: Em At, a21 = a12, a31 = a13 e a32 = a23.
Também neste caso B = Bt. B é uma matriz simétrica.
Aplicando os conceitos

“Virtude é manter-se cordeiro numa terra de lobos.”
(Robison Sá)
Referências bibliográficas
SOUZA, Joamir Roberto de. Novo Olhar Matemática. – 1 ed. – São Paulo: FTD, 2010. – (Coleção novo olhar; v. 2)
YOUSSEF, Antonio Nicolau. Matemática: ensino médio, volume único / Antonio Nicolau Youssef, Elizabeth Soares, Vicente Paz Fernandez. – São Paulo: Scipione, 2005.
Texto originalmente publicado em https://www.infoescola.com/matematica/transposicao-de-matrizes/