Trinômio Quadrado Perfeito e sua fatoração

O leitor já deve estar familiarizado com a nomenclatura Trinômio Quadrado Perfeito, neste artigo, substituída pela sigla TQP. Mas será que você conhece o mecanismo simples de fatoração do TQP? Saberá reconhecer um TQP assim que o ver? Não se preocupe. Neste trabalho abordarei detalhadamente este assunto, especificamente sobre o quadrado da diferença e da soma de dois termos, e, ao seu final, tenho a certeza de que fatorar e resolver TQPs não serão problemas para o caro estudante.

A fatoração foi desenvolvida na Europa, com ênfase nos séculos XVI e XVII. Nessa época, diante das múltiplas possibilidades de resolução de expressões que ela apresentava, matemáticos se apossaram desse conhecimento para resolver problemas. A fatoração está ligada a álgebra, e esta nasceu a partir de matemáticos árabes por volta do século IX. Nessa mesma época, o matemático Al-Khowarizmi divulgava importante obra relacionada à resolução de problemas envolvendo heranças.

Com o passar do tempo, as dificuldades de representar os cálculos matemáticos foram sendo extintas, principalmente pela chegada da álgebra, que possibilitou as representações de operações e valores desconhecidos por meio de letras e símbolos de melhor compreensão.

O Trinômio Quadrado Perfeito

Preste atenção nas definições que se seguem, pois a partir delas começaremos a discutir as características do Trinômio Quadrado Perfeito (TQP).

• O quadrado da soma de dois termos é igual ao quadrado do primeiro termo, mais duas vezes o primeiro termo vezes o segundo, mais o quadrado do segundo termo.

(x + 3)² = 0

 (x + 3).(x + 3) = 0

→ x² + 2 . x . 3 + 3² = 0

x² + 6x + 9 = 0

• O quadrado da diferença de dois termos é igual ao quadrado do primeiro termo, menos duas vezes o primeiro termo vezes o segundo, mais o quadrado do segundo termo.

(x - 3)² = 0

(x - 3).(x - 3) = 0

→ x² - 2 . x . 3 + 3²

x² - 6x + 9 = 0

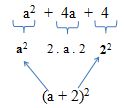
Uma dica importante para reconhecer um TQP é ficar de olho em sua estrutura. Note que ele sempre aparecerá, implícita ou explicitamente, de acordo com o formato exposto anteriormente.

Observe:

Após reconhecer a estrutura do TQP poderemos escrevê-lo na forma fatorada. É possível, mentalmente, descobrir se uma expressão é um Trinômio Quadrado Perfeito, basta que saibamos a sua estrutura, como no exemplo anterior.

Fatorando o TQP

Questão 1

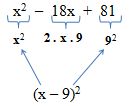
Fatore a expressão x² – 18x + 81.

Questão 2

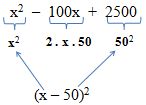
Encontre a forma fatorada do TQP: x² – 100x + 2500.

 “A educação é a ponte que nos leva ao sucesso.”

(Robison Sá)

Referência bibliográfica:
IMENES, LUIZ MÁRCIO; LELLIS, MARCELO. Matemática: 9º ano.  – 2 ed. – São Paulo: Moderna, 2012.