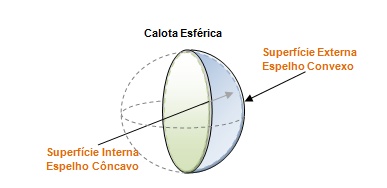
Espelho Convexo é caracterizado como sendo um espelho esférico, e pode ser considerado para qualquer superfície externa na forma de uma calota esférica que seja capaz de refletir a luz incidente, ou seja, o espelho convexo é uma “fatia” de uma esfera, essa fatia é chamada de calota esférica, e por isso conhecido de espelho esférico, e a parte que reflete (polida) é a parte externa dessa calota. Segue abaixo uma imagem que ilustra a formação de dois espelhos esféricos, um na parte externa da calota e outra na parte interna.
Figura 1 – Ilustra a forma de uma calota esférica e suas superfícies.
Comumente os espelhos convexos são utilizados para “prolongar” a visão, sendo assim podemos ver ângulos refletidos por eles que não conseguiríamos ver utilizando espelhos planos por exemplo. Com isso se costuma dizer que tais espelhos permitem ampliar o campo de visão. Geralmente esse tipo de espelho é encontrado em corredores de supermercado, farmácias, saídas de estacionamentos, retrovisores de veículos - para quem anda de ônibus já deve ter percebido logo acima das portas de saída, enfim entre outros lugares que necessitem ter uma visão prolongada do ambiente.
Figura 2 – Ilustra a visão circular do espelho convexo.
Na figura 2 a parte em negrito destaca uma visão 2D do espelho convexo na calota esférica, na figura temos o raio (R) que é a medida conhecida como Raio de Curvatura do espelho, sendo definido como a distância medida da superfície externa do espelho até o centro (C), que é conhecido como Centro de Curvatura, o ponto (C) coincide com o centro da esfera que originou o espelho.
Nos espelhos esféricos também temos o conhecido Ponto Focal (F), que é um ponto médio entre o centro e a curvatura do espelho, esse ponto médio fica sobre a reta (R), o ponto (F) é o local para onde os raios refletidos ou prolongados se convergem.
A medida entre o ponto focal e o vértice do espelho é a Distância Focal(f), como vimos o ponto focal fica localizado no ponto médio entre o centro de curvatura e o vértice do espelho, assim podemos afirmar que a distância focal pode ser definida como a metade da medida do raio:
O vértice (V) é ponto tangencial descrito na curvatura do espelho, e fica localizado sobre o eixo (e) do espelho, o eixo está representado como uma linha de centro no espelho que une o centro de curvatura, o foco e o vértice. Abaixo podemos ver cada dos elementos do espelho esférico na figura 3:
Figura 3 – Elementos de um espelho esférico.
Existe ainda outra propriedade para o espelho esférico que trata de sua condição de nitidez, que foi muito estuda por Gauss. Para que um espelho tenha uma característica de nitidez considerável é necessário que seu ângulo de abertura seja pequeno, inferior a 10 graus como limite máximo.
Figura 4 – Ilustra o ângulo de abertura máximo para condição de nitidez.
O ângulo de abertura é dado por dois segmentos de reta que interligam o centro de curvatura até as extremidades do espelho, como visto na figura 4. Quando esse limite é respeitado à equação (1) se torna válida. Gauss ainda afirmou que os raios incidentes devem ser próximos ao eixo principal e pouco inclinados também, isso contribui para as imagens refletidas serem mais nítidas.
Figura 5 – Utilização de espelho convexo em estabelecimento.
Para determinarmos como são formadas as imagens em um espelho convexo, devemos conhecer o comportamento dos raios de luz incidentes, ou seja, quando atingem a superfície do espelho e refletem as imagens. É muito importante ser bem definido esse conceito pois auxilia muito a resolução de problemas, e poderá ser utilizado para os dois tipos de espelhos esféricos (côncavo e convexo).
Figura 6 – Ilustração dos Raios Incidentes em um espelho convexo.
Para a formação das imagens temos, por exemplo, a necessidade de apenas utilizarmos dois feixes de raios de luz incidentes no espelhos. Por esses dois raios, determinamos a posição da imagem refletida, tamanho, e característica.
Figura 7 – Ilustração dos Raios emanados do objeto incidentes no espelho formando a imagem.
Para o espelho convexo temos apenas um caso para a formação da imagem. Para um objeto (O) posicionado a frente do espelho, os raios R¹ e R² emitidos do objeto incidem no espelho e esses refletem de acordo com o comportamento que vimos anteriormente. No encontro do prolongamento dos raios, temos a formação da Imagem, que no caso é caracterizada como sendo Virtual (pois é constituída pelo prolongamento dos raios incidentes, outra característica é que tal imagem não é constituída por luz na formação), Direita (mesma direção do objeto) e Reduzida (porque é menor que o objeto).
Fontes:
http://www.zeusdobrasil.com.br/site/int/produtos.asp?id_cat=81
Nussenzveig, H. M. – Curso de Física Básica: Ótica, Relatividade e Fisica Quântica; vol.4. São Paulo: Blucher 1998.
Halliday, David; Resnick, Robert; Walker Jearl; trad. de Biasi, Ronaldo Sérgio. Fundamentos de Física. vol.4. Rio de Janeiro: LTC, 2003.