Lentes Divergentes são corpos transparentes limitado por duas superfícies refratoras com um eixo central em comum.
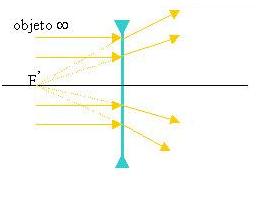
Quando um raio luminoso paralelo atinge uma lente, sofre uma refração mudando sua direção, essa refração nas lentes divergentes faz com que os raios se afastem do eixo central .
As lentes divergentes fornecem sempre uma imagem virtual, direita e menor sendo muito utilizadas no tratamento de miopia e em olhos mágicos instalados nas portas.
Figura 1 : Raios luminosos após atravessar uma lente divergente
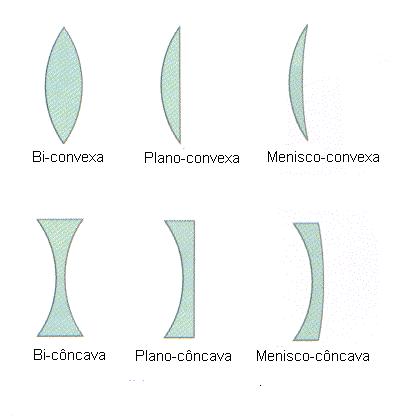
Nos casos mais comuns as lentes que apresentam as extremidades mais espessas do que a parte central (lentes Bi côncavas, plano concavas e convexo–concava ) são divergentes.
Existem também os casos especiais, onde o índice de refração do meio é maior que o índice de refração da lente convexa tornando=as divergentes.
Figura 2 : Tipos de lentes
Foco da lente divergente
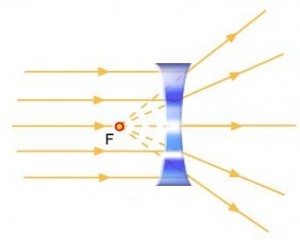
Quando um feixe de luz incide em uma lente divergente, paralelamente ao seu eixo, os raios luminosos, após atravessá-la divergem de tal modo que seus prolongamentos se encontram sobre um ponto ‘F’, sendo esse o seu 1º foco , a distancia de ‘F’ a lente,é denominada de distancia focal f .
Figura 3: Foco de uma lente divergente
O foco da lente divergente pode ser encontrado através da equação:
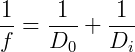
Onde por convenção:
- f - foco da lente divergente (para lente divergente f < 0)
- D0 - Imagem real
- Di - Imagem Virtual
Equação dos fabricantes de lentes
O meio que envolve a lente e o raio de curvatura influencia qualitativamente o valor da distancia focal. O estudo quantitativo desses fatores pode ser feito por meio da equação denominada “Equação dos fabricantes de lentes”.
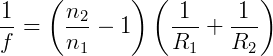
Considerando:
- R1 - raio de curvatura da superfície da lente mais próxima do objeto;
- R2 - raio de curvatura da outra superfície;
- n1 - índice de refração do meio que a envolve;
- n2 - índice de refração da lente.
Para a equação adota-se: o sinal do raio de curvatura é positivo quando a superfície externa que limita a lente for convexa e negativa quando for côncava, o raio será ∞ se a superfície for plana fazendo com que a fração 1/R = 0.
De acordo com a equação podemos chega na seguinte afirmação:
Uma lente pode produzir uma imagem de um objeto porque é capaz de desviar os raios luminosos, mas só é capaz de desviar os raios luminosos se tiver um índice de refração diferente do índice do meio.
Referências bibliográficas:
Halliday,Resnick.Fundamentos de Física vol 4 , 8º ed ,editora LTC, Rio de Janeiro ,2009.
Alvarenga,Beatriz.Maximo,Antônio,Física vol 2 , 1º ed ,editora Scipione,São Paulo, 2006.
Texto originalmente publicado em https://www.infoescola.com/optica/lentes-divergentes/