O ciclo de Born-Haber é considerado uma das aplicações da Lei de Hess (para a determinação da variação de entalpia de uma reação), onde através dele pode-se mensurar de forma indireta (utilizando-se de outras variáveis) a entalpia reticular de um composto iônico.
A entalpia reticular pode ser definida como a energia liberada por íons no estado gasoso ao se combinarem e formarem um produto no estado sólido, ou ainda, como a energia necessária para que um composto iônico seja decomposto a íons gasosos. Um bom exemplo é a determinação dessa entalpia para o composto LiF (fluoreto de lítio):
A energia reticular associada ao LiF(s) pode ser expressa através da equação:
- LiF(s) → Li+(g) + F-(g) ΔHf = ULiF
De modo semelhante, a entalpia de formação do LiF(s) a partir de lítio sólido e flúor gasoso é dado pela equação:
- Li(s) + ½F2(g) → LiF(s) ΔHf = -594,1 KJ
Analisando-se a transformação do lítio e do flúor em íons gasosos, são obtidos os seguintes valores de variação entálpica:
1) Para o lítio, constituem os processos de sublimação (passagem para o estado gasoso) e ionização (perda de um elétron):
- Li(s) → Li(g) ΔHs = 155,2 KJ
- Li(g) → Li+(g) + 1e- ΔHI1 = 520,0 KJ
2) Para o flúor, constituem os processos de dissociação (separação da molécula pela quebra da ligação) e também ionização (mas, com ganho de elétron):
- ½F2(g) → F(g) ΔHd = ½ ΔH0d = 150,6/2 = 75,3 KJ
- F(g) + 1e- → F-(g) ΔHAF1 = -328,0 KJ
Após estes passos, a reação entre os íons é expressa por:
- Li+(g) + F-(g) → LiF(s) ΔHf = - ULiF
Utilizando-se da lei de Hess, a soma das variações de entalpia de cada etapa intermediária resulta na variação de entalpia da reação final como se ela ocorresse em uma única via, portanto, a entalpia de formação do LiF(s) é igual à soma da entalpia de sublimação e ionização do lítio sólido, da dissociação e ionização (medida pela afinidade eletrônica, uma vez que recebe um elétron) do flúor mais a energia reticular associada ao composto. Ou seja:
- ΔHf = ΔHs + ΔHI1 + ΔHd + ΔHAF1 - ULiF
- -594,1 = 155,2 + 520 + 75,3 - 328 - ULiF
- -594,1 = 422,5 - ULiF
- ULiF = 1.016,6 KJ
Portanto, a entalpia reticular do fluoreto de lítio é igual a 1.016,6 KJ/mol, assim, para que possamos transformar este composto em íons no estado gasoso devemos fornecer, pelo menos, tal quantidade de energia (proporcionalmente à quantidade de matéria).
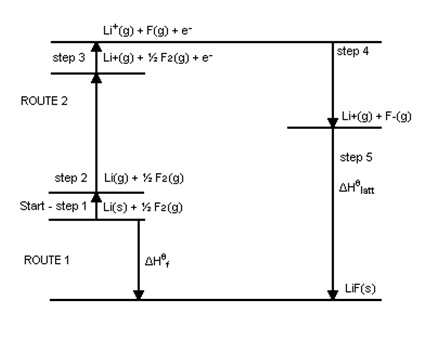
O esquema abaixo representa de modo semelhante todo o processo de determinação de ULiF seguido:
 Bibliografia:
Bibliografia:
http://www.aridesa.com.br/servicos/click_professor/alexandre_lima/Ciclo_de_Born_Haber.pps (visualização em 08/01/2011)
Texto originalmente publicado em https://www.infoescola.com/reacoes-quimicas/ciclo-de-born-haber/